- 들어가기 전에
소수 [Prime Number]
소수의 정의는 1보다 큰 자연수 중 1 과 그 수 자기 자신만을 약수로 갖는 자연수를 의미한다는 점은 누구나 알고 있을 것이다.
즉, 소수의 약수는 2개만을 갖고, 그 중 하나는 반드시 1 이며, 나머지는 자기 자신만을 약수로 갖기 때문에 만약 1 보다 크고 자기 자신의 수보다 작은 자연수를 약수로 갖게 된다면 이는 합성수라고 한다.
그리고 위의 개념을 확장해본다면 합성수는 3개 이상인 자연수의 곱으로 이루어져 있으며 소수로 이루어진 곱으로 표현할 수 있다.
그리고 이를 소인수분해라고 한다.
더욱 개념을 넓혀볼까.
소수는 1과 자기 자신만을 약수로 갖고, 합성수는 3개 이상인 자연수의 곱으로 이루어져 있으며 소수들로 이루어진 곱으로 표현할 수 있다고 했다.
1 보다 큰 자연수는 모두 소수 또는 합성수로 이루어져 있으니 1 보다 큰 모든 자연수는 소수들의 곱으로 표현할 수 있다.
이렇듯 소수는 수학적으로도 매우 중요한 개념이다.
그렇다면 왜 개발자 입장에서 또는 프로그래밍의 세계에서 소수가 중요한 이유는 무엇일까.
바로 "암호" 때문이다.
실제로 우리 일상생활에서도 많이 쓰이는 암호 또한 소수를 이용하고 있다.
대표적으로 'RSA 암호화 방식'이 있다.
위 암호화 방식의 가장 근본적인 접근 방식은 이렇다.
"임의의 수들의 곱은 구하기 쉽지만 역으로 소인수 분해하는 것은 어렵다."
즉, 𝑝 × 𝑞 = 𝐍 를 만들기는 쉽지만, 𝐍 을 역으로 소인수 분해하여 𝑝 × 𝑞 를 만족하는 수를 찾기가 어렵다는 것이다.
예로 들어보자.
77 을 소인수분해 하면?
7 × 11 이 바로 나온다.
그렇다면 조금 더 큰 수라면 어떨까?
12126 을 소인수 분해 해보자.
먼저 직관적으로는 2로 나누어 떨어지겠다.
P × 2 = 12126 ... P = 6063
그리고 각 자릿수의 합 ( 6 + 0 + 6 + 3 ) 은 15 로 3의 배수이니 3으로 나누어 떨어지겠다.
P × 2 × 3 = 12126 ... P = 2021
그리고 2021 이 수를 소인수 분해를 해보자.
한 번에 눈에 들어오는가?
2021 을 소인수 분해하면 43 과 47 이다.
즉, 2부터 하나씩 대입해보려 하면 43 까지 대입해보아야 한다.
그리고 43과 47 은 각각 소수로 더이상의 소인수분해가 불가능 하다.
뭐 이정도 까진.. 컴퓨터의 대단한 연산능력에 맏기면 금방 풀릴 수 있겠다.
그런데 다음과 같은 수라면??
114381625757888867669235779976146612010218296721242362562561842935706935245733897830597123563958705058989075147599290026879543541
이 수는 실제로 RSA-129 의 공개키였고 현재는 풀린 129자리의 수다.
위 수를 여러분의 컴퓨터로 소인수 분해를 할 수 있겠는가?
일단 정답부터 말하자면 다음과 같다.
RSA-129 =
3490529510847650949147849619903898133417764638493387843990820577 × 32769132993266709549961988190834461413177642967992942539798288533
위의 두 수는 반드시 소수다.
위 문제를 컴퓨터로 푼다면 쉽게 풀릴 것 같지만 이는 오산이다.
실제로 위 문제를 풀기위해서 약 1600대의 컴퓨터와 600명의 사람이 모여 6개월동안 진행했다.
이 마저도 129자리 소수를 푸는데 저러한 시간이 걸렸는데 현재 암호방식은 RSA-2048로 617 자리수의 공개키가 있다.
617 자리의 수는 얼마나 오래 걸릴지 가늠이 안된다.
그래서 실제로도 대부분의 인터넷뱅킹도 RSA-2048 을 쓰고 있다.
혹시 독자 분들 중에 위 키를 푼다면 혹시 모를까... 세계 유명인사가 될 테니..
RSA-2048 의 공개키를 공유하겠다.
RSA-2048 =
25195908475657893494027183240048398571429282126204032027777137836043662020707595556264018525880784406918290641249515082189298559149176184502808489120072844992687392807287776735971418347270261896375014971824691165077613379859095700097330459748808428401797429100642458691817195118746121515172654632282216869987549182422433637259085141865462043576798423387184774447920739934236584823824281198163815010674810451660377306056201619676256133844143603833904414952634432190114657544454178424020924616515723350778707749817125772467962926386356373289912154831438167899885040445364023527381951378636564391212010397122822120720357
(화이팅입니다...)
서론이 너무 길었다.. 여튼 소수는 우리 일상생활에서도 긴밀하게 쓰이고 있다.
그런김에 소수를 구하고 판별하는 몇가지 방법을 같이 배워보고자 한다.
각 방법마다 소수를 판별하는 알고리즘과,
N 이하의 소수를 모두 구하는 알고리즘을 소개하겠다.
- 방법 1
" N 보다 작은 자연수들로 모두 나눠본다. "
가장 기본적인 방법이라 할 수 있겠다.
임의의 수 N 이 1 과 N 을 제외한 다른 수를 약수로 갖고 있다면 그 수는 소수가 아니고, 만약 다른 약수가 없다면 그 수는 소수일 것이다.
[ 소수 판별 알고리즘 ]
|
|
import java.util.Scanner; |
|
|
|
|
|
public class Prime_1 { |
|
|
public static void main(String[] args) { |
|
|
|
|
|
Scanner in = new Scanner(System.in); |
|
|
|
|
|
is_prime(in.nextInt()); |
|
|
|
|
|
} |
|
|
|
|
|
// 소수 판별 메소드 |
|
|
public static void is_prime(int number) { |
|
|
|
|
|
// 0 과 1 은 소수가 아니다 |
|
|
if(number < 2) { |
|
|
System.out.print("소수가 아닙니다"); |
|
|
return; |
|
|
} |
|
|
|
|
|
// 2 는 소수다 |
|
|
if(number == 2) { |
|
|
System.out.print("소수입니다"); |
|
|
return; |
|
|
} |
|
|
|
|
|
|
|
|
for(int i = 2; i < number; i++) { |
|
|
|
|
|
// 소수가 아닐경우 |
|
|
if(number % i == 0) { |
|
|
System.out.print("소수가 아닙니다"); |
|
|
return; |
|
|
} |
|
|
} |
|
|
// 위 반복문에서 약수를 갖고 있지 않는경우 소수다. |
|
|
System.out.print("소수입니다"); |
|
|
return; |
|
|
} |
|
|
|
|
|
|
|
|
} |
2 이상 N 미만의 수 중에 나누어 떨어지는 수가 존재한다면 소수가 아님을 이용한 소수 판별법이다.
또한, 위 알고리즘의 시간복잡도는 당연히 N 이하의 수까지 모든 수를 검사하므로 O(N) 이다.
[ N 이하의 모든 소수 구하는 알고리즘 ]
위를 응용하여 N 이하의 소수를 모두 구하는 알고리즘은 다음과 같을 것이다.
|
|
// 소수만 출력 |
|
|
|
|
|
import java.util.Scanner; |
|
|
|
|
|
public class Prime_1 { |
|
|
public static void main(String[] args) { |
|
|
|
|
|
Scanner in = new Scanner(System.in); |
|
|
|
|
|
int N = in.nextInt(); |
|
|
|
|
|
// 0 ~ N 까지 수 중 소수를 구하는 반복문 |
|
|
for(int i = 0; i <= N; i++) { |
|
|
make_prime(i); |
|
|
} |
|
|
|
|
|
} |
|
|
|
|
|
// 소수 생성 메소드 |
|
|
public static void make_prime(int number) { |
|
|
|
|
|
// 0 과 1 은 소수가 아니므로 종료 |
|
|
if(number < 2) { |
|
|
return; |
|
|
} |
|
|
|
|
|
// 2 는 소수다 |
|
|
if(number == 2) { |
|
|
System.out.println(number); |
|
|
return; |
|
|
} |
|
|
|
|
|
|
|
|
for(int i = 2; i < number; i++) { |
|
|
|
|
|
// 소수가 아닐경우 종료 |
|
|
if(number % i == 0) { |
|
|
return; |
|
|
} |
|
|
} |
|
|
// 위 반복문에서 약수를 갖고 있지 않는경우 소수다. |
|
|
System.out.println(number); |
|
|
return; |
|
|
} |
|
|
|
|
|
|
|
|
} |
위 알고리즘은 소수 판별 알고리즘을 N 번 반복하여 각 수마다 소수 판별 한 뒤 소수만 출력하도록 한 알고리즘이다.
즉 O(N) 알고리즘을 N 번 반복하므로 위 방법의 N 이하의 소수를 모두 구하는 알고리즘의 시간복잡도는 O(N²) 이다.
- 방법 2
" √N 이하의 자연수들로 모두 나눠본다. "
방법 1 의 방법에서 약간 업그레이드 된 알고리즘이다.
바로 N 을 √N 이하의 자연수들만 나누는 방법이다.
왜 √N 이하의 자연수들만 나누면 되는지는 생각보다 매우 쉽게 알 수 있다.
생각해보자. 소수를 판별한다는 것은 결국 1 과 자기 자신을 제외한 다른 자연수를 약수로 갖고 있으면 안된다는 의미다.
임의의 자연수 𝐍 (𝐍 > 0) 이 있다고 가정하자.
𝑝 × 𝑞 = 𝐍 을 만족할 때 우리는 아래와 같은 부등식을 완성할 수 있다.
( 1 ≤ 𝑝 , 𝑞 ≤ 𝐍 )
그리고 𝑝 와 𝑞 중 하나는 √N 보다 작거나 같다.
예로들어 𝐍 = 16 라고 하자.
그러면 아래와 같이 두 수의 곱으로 표현할 수 있다.
1 × 16
2 × 8
4 × 4
8 × 2
16 × 1
여기서 볼 수 있듯이 만약 𝑝 가 증가한다면 자연스레 𝑞 가 감소하고,
반대로 𝑝 가 감소한다면 자연스레 𝑞 가 증가한다.
그리고 𝑝 와 𝑞 는 𝐍의 약수이기 때문에 결국 𝐍 을 임의의 수로 나누게 되면 임의의 수가 √N 보다 작다면 결국 나머지는 √N 보다 클 수 밖에 없다.
결과적으로 𝑝 와 𝑞 중 하나는 반드시 √N 보다 작거나 같다.
즉, √N 이하의 자연수 중에 나누어 떨어지는 수가 있다면 이는 1 과 N 을 제외한 다른 자연수가 N 의 약수라는 의미이므로 소수가 아니게 되는 것이다.
그럼 이를 토대로 알고리즘을 짜보자.
[ 소수 판별 알고리즘 ]
|
|
import java.util.Scanner; |
|
|
|
|
|
public class Prime_2 { |
|
|
public static void main(String[] args) { |
|
|
|
|
|
Scanner in = new Scanner(System.in); |
|
|
|
|
|
is_prime(in.nextInt()); |
|
|
|
|
|
} |
|
|
|
|
|
// 소수 판별 메소드 |
|
|
public static void is_prime(int number) { |
|
|
|
|
|
// 0 과 1 은 소수가 아니다 |
|
|
if(number < 2) { |
|
|
System.out.print("소수가 아닙니다"); |
|
|
return; |
|
|
} |
|
|
|
|
|
// 2 는 소수다 |
|
|
if(number == 2) { |
|
|
System.out.print("소수입니다"); |
|
|
return; |
|
|
} |
|
|
|
|
|
// 제곱근 함수 : Math.sqrt() |
|
|
for(int i = 2; i <= Math.sqrt(number); i++) { |
|
|
|
|
|
// 소수가 아닐경우 |
|
|
if(number % i == 0) { |
|
|
System.out.print("소수가 아닙니다"); |
|
|
return; |
|
|
} |
|
|
} |
|
|
// 위 반복문에서 약수를 갖고 있지 않는경우 소수다. |
|
|
System.out.print("소수입니다"); |
|
|
return; |
|
|
} |
|
|
|
|
|
|
|
|
} |
2 이상 √N 이하의 수 중에 나누어 떨어지는 수가 존재한다면 소수가 아님을 이용한 소수 판별법이다.
또한, 위 알고리즘의 시간복잡도는 당연히 √N 이하의 수까지 모든 수를 검사하므로 O(√N) 이다.
[ N 이하의 모든 소수 구하는 알고리즘 ]
위를 응용하여 N 이하의 소수를 구하는 알고리즘은 다음과 같을 것이다.
|
|
// 소수만 출력 |
|
|
|
|
|
import java.util.Scanner; |
|
|
|
|
|
public class Prime_2 { |
|
|
public static void main(String[] args) { |
|
|
|
|
|
Scanner in = new Scanner(System.in); |
|
|
|
|
|
int N = in.nextInt(); |
|
|
|
|
|
// 0 ~ N 까지 수 중 소수를 구하는 반복문 |
|
|
for(int i = 0; i <= N; i++) { |
|
|
make_prime(i); |
|
|
} |
|
|
|
|
|
} |
|
|
|
|
|
// 소수 생성 메소드 |
|
|
public static void make_prime(int number) { |
|
|
|
|
|
// 0 과 1 은 소수가 아니므로 종료 |
|
|
if(number < 2) { |
|
|
return; |
|
|
} |
|
|
|
|
|
// 2 는 소수다 |
|
|
if(number == 2) { |
|
|
System.out.println(number); |
|
|
return; |
|
|
} |
|
|
|
|
|
|
|
|
// 제곱근 함수 : Math.sqrt() |
|
|
for(int i = 2; i <= Math.sqrt(number); i++) { |
|
|
|
|
|
// 소수가 아닐경우 종료 |
|
|
if(number % i == 0) { |
|
|
return; |
|
|
} |
|
|
} |
|
|
// 위 반복문에서 약수를 갖고 있지 않는경우 소수다. |
|
|
System.out.println(number); |
|
|
return; |
|
|
} |
|
|
|
|
|
|
|
|
} |
위 알고리즘은 소수 판별 알고리즘을 N 번 반복하여 각 수마다 소수 판별 한 뒤 소수만 출력하도록 한 알고리즘이다.
즉 O(√N) 알고리즘을 N 번 반복하므로 위 방법의 N 이하의 소수를 모두 구하는 알고리즘의 시간복잡도는 O(N√N) 이다.
- 방법 3 : 에라토스테네스의 체
소수를 구하는 대표적인 방법 중 하나다.
" k=2 부터 √N 이하까지 반복하여 자연수들 중 k를 제외한 k의 배수들을 제외시킨다"
즉, 방법으로 보면 다음과 같다.
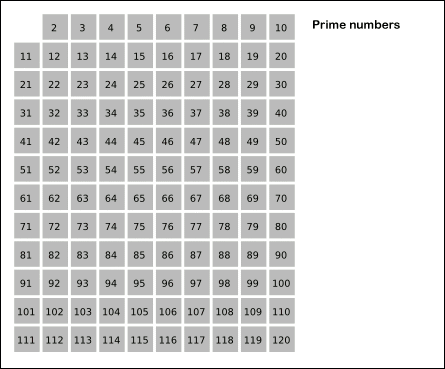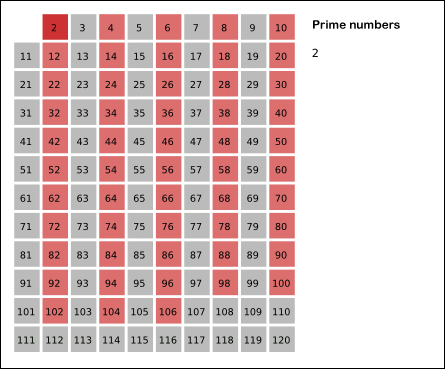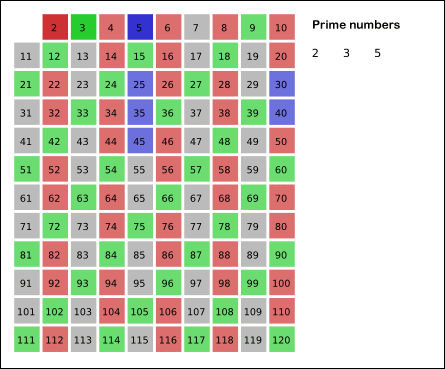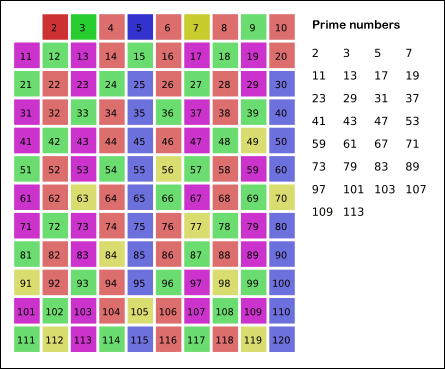
k = 2 이면 2 를 제외한 2의 배수를 모두 지워주고,
k = 3 이면 3 을 제외한 3의 배수를 모두 지워주고,
(4는 이미 k = 2 에서 제외되어 넘어간다.)
k = 5 이면 5 를 제외한 5의 배수를 모두 지워주고..
이렇게 하여 k = √N 까지 반복하는 방법이다.
이 방법은 소수를 구하는 방법이랑 판별하는 방법이 동일하기 때문에 하나로 묶어서 설명하겠다.
[ N 이하의 모든 소수를 구하는 알고리즘 ]
|
|
import java.util.Scanner; |
|
|
|
|
|
public class Prime_3 { |
|
|
|
|
|
public static boolean[] prime; // 소수를 체크할 배열 |
|
|
public static void main(String[] args) { |
|
|
|
|
|
Scanner in = new Scanner(System.in); |
|
|
|
|
|
int N = in.nextInt(); |
|
|
|
|
|
make_prime(N); |
|
|
|
|
|
for(int i = 0; i < prime.length; i++) { |
|
|
if(prime[i] == false) { // 소수(false)일 경우 출력 |
|
|
System.out.println(i); |
|
|
} |
|
|
} |
|
|
} |
|
|
|
|
|
// N 이하 소수 생성 메소드 |
|
|
public static void make_prime(int N) { |
|
|
|
|
|
prime = new boolean[N + 1]; // 0 ~ N |
|
|
|
|
|
/* |
|
|
소수가 아닌 index = true |
|
|
소수인 index = false |
|
|
*/ |
|
|
|
|
|
// 2 미만의 N 을 입력받으면 소수는 판별할 필요 없으므로 바로 return |
|
|
if(N < 2) { |
|
|
return; |
|
|
} |
|
|
|
|
|
prime[0] = prime[1] = true; |
|
|
|
|
|
|
|
|
// 제곱근 함수 : Math.sqrt() |
|
|
for(int i = 2; i <= Math.sqrt(number); i++) { |
|
|
|
|
|
// 이미 체크된 배열이면 다음 반복문으로 skip |
|
|
if(prime[i]==true) { |
|
|
continue; |
|
|
} |
|
|
|
|
|
// i 의 배수들을 걸러주기 위한 반복문 |
|
|
for(int j = i*i; j < prime.length; j = j+i) { |
|
|
prime[j] = true; |
|
|
} |
|
|
} |
|
|
|
|
|
} |
|
|
|
|
|
} |
언뜻 보기에는 이중for문이라 시간복잡도가 O(N²) 일 것 같지만 그렇지 않다.
1 ~ 𝑥 까지의 수가 있는 칸을 체크하는 횟수를 대략적으로 따진다면 아래와 같을 것이다.
(n = 1 부터 시작한다고 할 때)
(𝑥) + (𝑥/2) + (𝑥/3) + (𝑥/4) + (𝑥/5) + (𝑥/6) + ⋯ + 1
그러면 위 식을 다음과 같이 표현 할 수 있다.
𝑥(1 + 1/2 + 1/3 + ⋯ + 1/𝑥)
위의 x로 묶인 괄호 안의 수열은 조화 수(Harmonic Number)라고 하는데, 쉽게 말해서 조화 수열에서 부분 합을 말한다고 생각하면 된다.
그리고 다음과 같이 발산하게 된다고 한다.
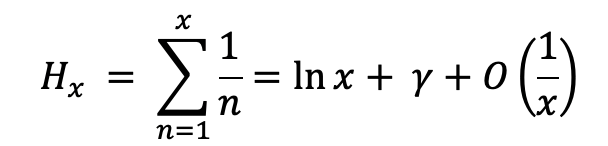
이 때 감마는 상수 값이고 O(1/x)는 우리가 생각하는 big O와 같은 표기로 수학에서는 함수 성장률의 상한선이다. 그리고 위의 조화수는 대략 자연로그의 형태를 따라간다.
(자세한 건 아래 링크를 참고하시기 바란다.)
https://en.wikipedia.org/wiki/Harmonic_number
즉, N 이하의 소수에 대하여 체에 거르는 시간이 logN 이므로 단순하게 체에 거르는 것만 해도 시간 복잡도는 O(N㏒N) 이다.
( ㏒ 는 자연로그 𝑙𝑛 으로 본다 )
그런데 우리는 여기서 더 나아가 이미 체크된 배열은 검사하지 않고 다음 반복문으로 넘어간다.
(𝑥/2) + (𝑥/3) + (𝑥/4) + (𝑥/5) + (𝑥/6) + (𝑥/7)+ (𝑥/8)+ (𝑥/9) + ⋯ + (𝑥/𝑥-1)
우리는 앞서 조화수를 통해 점근적 시간 복잡도 O(NlogN) 이라는 시간 복잡도를 얻었다.
이 의미는 x개의 수에 대해 2일 때 체크하는 개수인 (x/2), 3일 때 체크하는 개수인 (x/3), ... 이렇게 체크를 하게 된다.
하지만 우리가 알고싶은 것은 이미 중복되는 수들은 검사하지 않는다는 것이다. 이 의미는 무엇일까? 결국 검사하는 수는 소수로 판정 될 때 그의 배수들을 지우는 것이라는 것이다. 이 말은 구간 내의 소수의 개수를 알아야 한다는 뜻이기도 하다.
근데, 소수가 규칙성이 있는가? 이 것은 아직까지도 풀지못한 것이다. 이를 찾고자 가우스는 15살 때 하나하나씩 구하면서 x보다 작거나 같은 소수의 밀도에 대해 대략 1 / ln(x) 라는 것을 발견하게 되는데 증명을 못했다. (이를 가우스의 소수 정리라고 한다)
즉, 위를 거꾸로 말하면 x번째 소수는 xlog(x) 라는 의미가 되지 않겠는가? 즉, 우리는 앞서 1/x 의 합을 구했지만, 실제로 중복되는 수가 제외된다면 x는 소수만 된다는 의미고, 이는 소수의 역수 합이다. (1/2 + 1/3 + 1/5 + 1/7 + ⋯ ) 이런식으로 말이다.
그러면 시간 복잡도를 도출해낼 수 있다.
바로 O(Nlog(log N)) 의 시간 복잡도를 갖게 된다.
'프로그래밍 & IT > Algorithm' 카테고리의 다른 글
| [알고리즘] 백준 2581번 소수 :: 우유 (0) | 2021.10.20 |
|---|---|
| [알고리즘] 백준 1978번 소수찾기 :: 우유 (0) | 2021.10.20 |
| [알고리즘] 백준 1712번 손익분기점 :: 우유 (0) | 2021.10.18 |
| [알고리즘] 백준 3052번 나머지 :: 우유 (0) | 2021.10.07 |
| [알고리즘] 백준 2562번 곱셈:: 우유 (0) | 2021.10.06 |